こんにちは、自由研究ラボ所長のヤベちゃんです。
今日はまとめ方の第2回と言うことでグラフの基本について説明したいと思います。
実験で得た、データを読んでいる人が見やすい形にするのがグラフです。
グラフにはいろんな種類があり、データによって適切なグラフが変わるのでしっかりみていきましょう!
棒グラフ
いくつかの項目を比べたいとき、使います。
例えば、1週間の雨の回数、〇〇した割合、〇〇を選んだ人数などを比べるときに便利です。
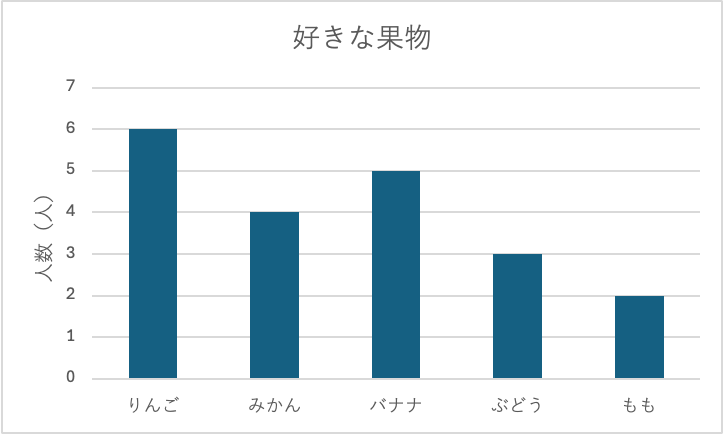
横軸に条件(今回の例だとフルーツの選択肢)、縦に各条件ごとの人数をとります。
折れ線グラフ
時間の流れで変化を見たいときには折れ線グラフを使います。
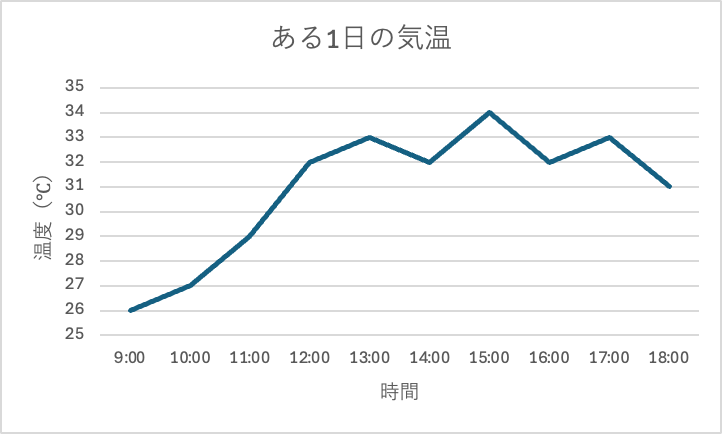
折れ線グラフでは、グラフの点同士を繋げるので、時間の流れによってデータが増えていたり減っていたりするのがすぐにわかります。
時間ごとに何かデータを計測していた場合は折れ線グラフを使うのがいいでしょう。
円グラフ
全体位の中で割合を見たいときに使います。
例えばアンケート調査などをしたときに「○人中◻︎人がAと答えた」のような結果があれば、円グラフを使いましょう。
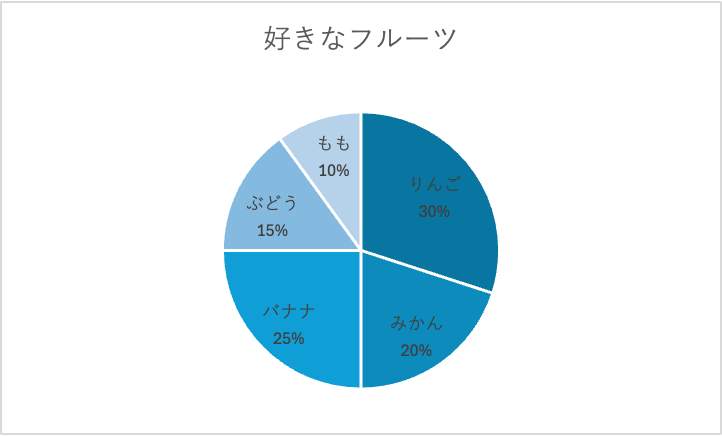
ちなみに%の計算方法は知っていますか?
例えば今回の例のように20人中6人がりんごが好きだったとすれば
6÷20×100=30
のように、ある数を全体数で割って100をかければ%を求めることができます。
ヒストグラム
データの分布(どの辺に固まっている?)がわかりやすいグラフです。
棒グラフと似ていますが、ヒストグラムの場合、横軸がバナナ、りんごのようなバラバラなものではなく、ある尺度(例えば大きさや時間など)で連続しています。
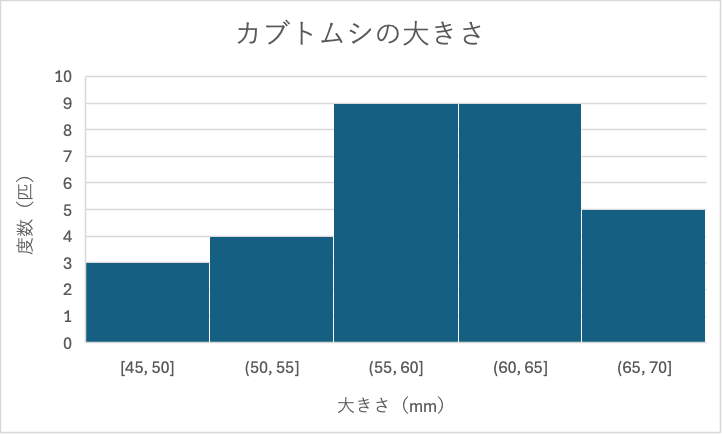
この例ではカブトムシの大きさが横軸になっています。
45mm〜50mmのカブトムシが三匹、50~55mmのカブトムシが4匹いたと言うことがわかります。
このグラフを見るとカブトムシの大きさは55〜60mmの間に多く分布していることがわかりますね!
散布図
散布図はある二つのデータの関係を見たいときに使います。
例えば、横軸を国語の点数、縦軸を算数の点数とすると下のようなグラフを書くことができます。
このグラフを見ると、なんとなく国語の点数が高い子は算数の点数も高いことがわかりますね!
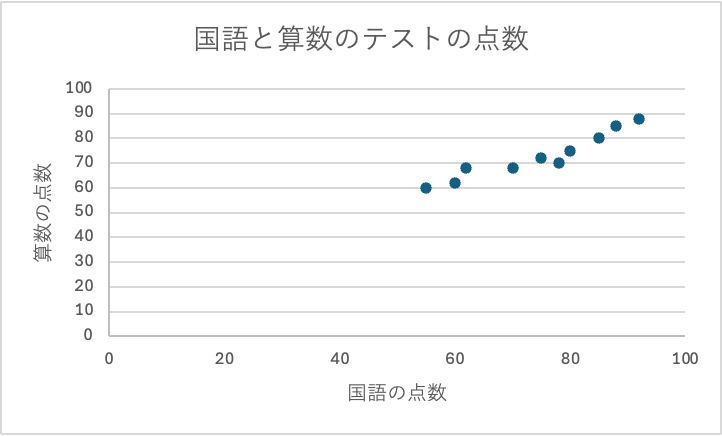
ちなみにこのデータの相関係数は0.70でした。
散布図を作ったら、ぜひ相関係数を計算して見ましょう。
計算方法は以下の記事にまとめてあります。
 第7回 自由研究まとめ方のコツ① データをまとめよう
第7回 自由研究まとめ方のコツ① データをまとめよう
まとめ
いかがだったでしょうか。
グラフと言ってもさまざまなものがあり、(まだ今日紹介したものだけではありません!)データによって正しいグラフを使うことが、わかりやすく実験をまとめる鍵になります。
また、これはすべてのグラフに共通することですが、グラフには必ず横軸と縦軸のラベルを入れましょう。
例えば縦軸はカブトムシの大きさ(mm)と言ったふうに、それぞれの軸が何を表していて、単位はどのくらいなのか。
これがないと全く意味のわからないグラフになってしまいます。
機会があれば、他のグラフについても紹介したいと思います。
今日はここまで!ではまた!

