こんにちは!自由研究ラボ所長のヤベちゃんです!
今回は、データのまとめ方について解説していきたいと思います。
皆さんが実験やアンケートなどでゲットしたデータはそのままでは意味を持ちません。
この記事を読んで適切なまとめ方を学びましょう!
内容的には中学、高校の内容ですが、小学生にもわかるように説明するのでぜひ最後までお読みください。
平均
「小学6年生の身長ってだいたいどれくらいですか?」
皆さんならこの問いになんと答えますか?
クラスにはきっと130cm代の子も、160cm、下手したら170cmを超えている子もいるかもしれません。
「小学6年生」という大きな括りの身長はなんて答えるべきなのでしょうか?
ここで考えるのが「代表値」という値です。
読んで字のごとく、そのグループの代表となる値です。
まずは一番有名な平均を考えてみましょう。
平均は全てのデータを足してデータ数で割った値のことです。
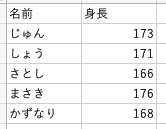
例えばこのようなデータがあった場合
平均=(166+171+176+168+173)÷5=170.8(cm)となります。
エクセルでの計算方法
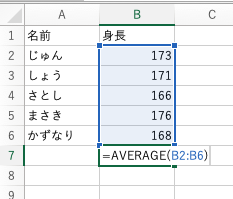
1表を作る
2=AVERAGE( と入力する
3平均を出したい部分のデータを選択する
4)で閉じる
これで計算することができます。
中央値
代表値2つ目は中央値です。
例えば、小学校6年生のクラスに2m15cmの子が一人いたらどうでしょう
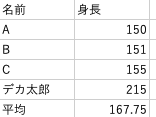
他の子はだいたい150cm台なのに、平均が167.75cmになってしまいました。
このように平均は一つ飛び抜けた値があると、少しおかしくなってしまうという弱点があります。
そこで、よく使われるのが中央値です。
中央値、つまり真ん中の値です。
データが奇数個の場合は真ん中の大きさのデータ、偶数この場合は真ん中の2つのデータの平均をとります。
今回の例で言うとB,Cが真ん中の二人なので151と155の間を撮って153cmが中央値となります。
エクセルで計算するときには
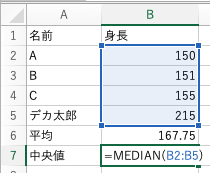
最頻値
もう一つ代表値の例を挙げるならば最頻値です。
最頻値とは最もよく出てきたデータのことです。
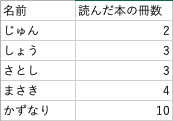
例のような場合、最頻値は3になります。
このグループの人の多くは3冊の本を読んでいると言えるわけです。
エクセルで計算するのも簡単です。
=MODE .SNGL()を使ってみてください

範囲
さて、ここからは範囲の話をします。
これは代表値とは異なり、データがどの程度散らばっているかを表します。
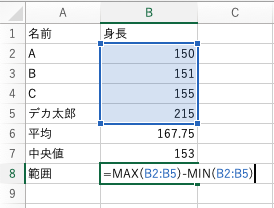
範囲は簡単で、一番大きいデータから一番小さいデータを引けばOKです!
エクセルでは以下のように
= MAX() – MIN()を使ってください。
データの中の最大値から最小値を引いてくれます。
分散・標準偏差
ここから難しくなります。
頑張ってついてきてください!
分散、標準偏差もデータの散らばりを表します。
例えば、平均が70点のテストでも一人一人の点数が69,69,69,70,70,70,70,71,71,71なのか、40,40,40,40,40,100,100,100,100,100なのかで意味が少し違うのは感覚的にわかるかと思います。
計算自体はややこしいのでこれはエクセルなどを使って計算してください。
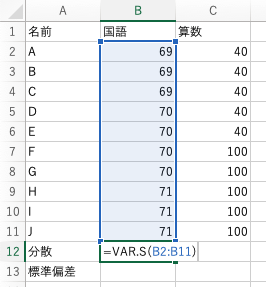
分散を求めるには=VAR.S()を使います。
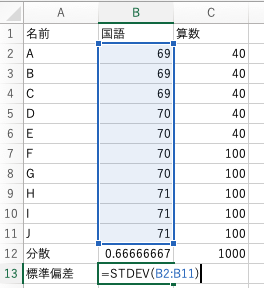
標準偏差を求めるには=STDEV()を使ってください。
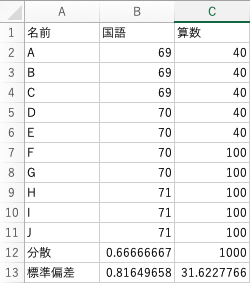
これが結果です。
散らばりが大きい方が分散と標準偏差が大きくなっていることが一目瞭然ですね。
これらのデータの使い方は後々説明しますが、小学生の自由研究の結果で平均の横に標準偏差のデータが載っていたら、それだけで学校の先生や審査員の方はかなり驚くと思います(小学校の先生じゃ、もしかしたら意味すら分からないかも。。。?)
少し難しかったと思いますが、研究に分散・標準偏差は欠かせません!
難しいと言っても、エクセルを使ってしまえば1発で出ますので「データの散らばり具合だ」ってことさえ分かっていればOKです!
相関係数
本日ラストは相関係数!
これまたかなり便利なものです。
二つのデータに関係性がどのくらいあるのかを測ります。
例えば、身長と体重、国語と算数の点数、入れた砂糖の量と甘いと感じた人の割合
どれもどちらかが増えればもう一方も増えそうな気はします。
それを数字で示すためのものが相関係数です。
エクセルでの求め方はこうです。
=CORRELを使って、最初にデータ1(今回は国語の点数)、カンマ(,)を挟んでデータ2(今回は算数の点数)を入れます。
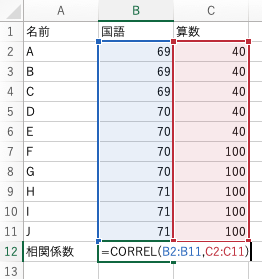
結果は0.77でした。
相関係数は以下のような意味があります。
| 数字(相関係数) | どんな関係? | 説明 |
|---|---|---|
| +1 に近い | とても強い「同じ動き」 | どっちも一緒に増えたり減ったりする(友だちみたい) |
| +0.7~+0.9 | けっこう強い関係 | だいたい一緒に増える感じ |
| +0.4~+0.6 | ちょっと関係あり | なんとなくつながってそう |
| 0(ゼロ) | 関係なし | バラバラ。関係なさそう |
| −0.4~−0.6 | ちょっと逆の動き | 片方が増えると、もう片方が減るかも |
| −0.7~−0.9 | けっこう逆の動き | だいたい逆の動きをしてる |
| −1 に近い | とても強い「逆の動き」 | 一方が増えると必ずもう一方が減る(ケンカしてる?) |
今回は0.77なので結構強い関係があると言うことがわかりました!
相関係数を使って自由研究をまとめることができたらパーフェクト!
学校の先生、ぐうの音も出ません。
相関係数は先ほど例に出した身長と体重、国語と算数の点数、入れた砂糖の量と甘いと感じた人の割合などいろんなデータについて考えることができますので、是非使ってください。
まとめ
いかがだったでしょうか。
結構難しい話もありましたが、エクセルを使えばなんとかできそうじゃないですか?
エクセルが難しいなと思ったら、それこそChatGPTにデータを入力して「平均と分散を出して(計算にはPythonを使ってください)」と打ち込めば正しい答えが帰ってきます!
同じ実験結果でも、どのようにまとめるかで自由研究の完成度はかなり変わります。
ぜひ、レベルの高いまとめ方をしてください!
ではまた!



